Research

Floquet topological states

Topology is one of the key concepts in modern condensed matter physics. It was believed that "topology is robust against perturbation" and is something that is fixed when a material is synthesized. We found a way to change the topology of materials dynamically. In 2009, we found a theoretical model in which the Berry curvature, Chern number, and the chiral edge state could be controlled or induced by external time-periodic fields such as a laser. The key idea is that electrons become photo-dressed. They are described by Floquet states, a temporal analog of Bloch states, and the topology of the quasi-energy bands can be changed as a function of the laser intensity, polarization, and frequency.

Figure: (Left) Honeycomb lattice in circularly polarized laser becomes a Floquet Chern insulator.
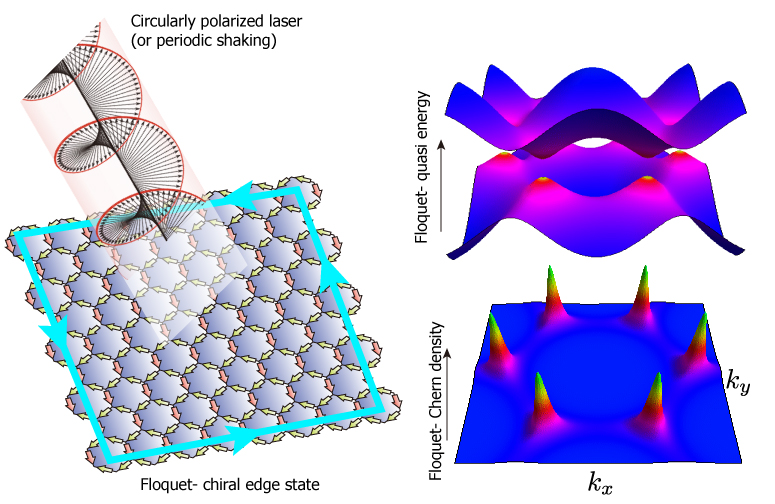
(Right) The Floquet quasi-energy in the high frequency limit shows a gap opening at the Dirac points. This leads to the emergence of the Floquet Berry curvature.

Nonequilibrium theory of strongly correlated electrons

We have worked on the physics of strongly correlated electron systems far from equilibrium. This has been done in collaboration with Naoto Tsuji, Martin Eckstein, and Philipp Werner, which led to the extension of nonequilibrium dynamical mean field theory[Aoki, et al. RMP'14]